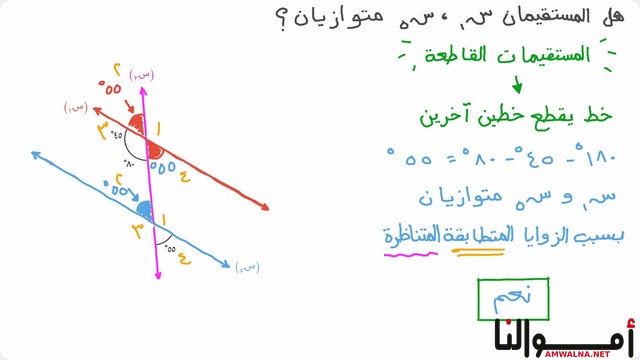
بحث عن إثبات توازي مستقيمين

في الرياضيات يُعتبر مفهوم التوازي بين المستقيمات من المواضيع الأساسية التي تسهم في فهم البناء الهندسي للأشكال، ويتعلق بعدم تقاطع المستقيمين مهما امتدا في الاتجاه نفسه، ويعد من المفاهيم الجوهرية في علم الهندسة المستوية، حيث يُستخدم بشكل واسع في حل المسائل الرياضية المتعلقة بالأشكال الهندسية والخطوط.

عناصر بحث عن إثبات توازي مستقيمين

• المقدمة.
• خصائص المستقيمات المتوازية.
• طرق إثبات توازي مستقيمين.
• أمثلة تطبيقية على إثبات توازي مستقيمين.
• التطبيقات العملية لتوازي المستقيمات في الحياة اليومية.
• تطبيقات إثبات التوازي في الرياضيات والعلوم.
• استخدام البرهان الرياضي لإثبات توازي مستقيمين.
• الخاتمة.
• يُمكنك تحميل البحث بصيغة pdf عبر الأيقونة التالية:

مقدمة بحث عن إثبات توازي مستقيمين

يعد فهم توازي المستقيمات أمراً أساسياً في حل المسائل الهندسية، ويتيح لنا استخدام مجموعة متنوعة من النظريات لإثبات توازي المستقيمات كذلك، فإن معرفة خواص المستقيمات المتوازية تساعد في التطبيقات العملية للعديد من المجالات الهندسية.

المستقيمان المتوازيان هما مستقيمان يقعان في المستوى نفسه ولا يتقاطعان مهما امتدا و يمكننا التعبير عن هذا المفهوم بطريقتين: إما بتحديد الخطوط المستقيمة المتوازية على أساس ميلها المتساوي أو باستخدام المسافة الثابتة بينهما.

خصائص المستقيمات المتوازية

1. تساوي الزوايا المقابلة: إذا تقاطع مستقيمان متوازيان مع قاطع، فإن الزوايا المتقابلة تكون متساوية.
2. تساوي الزوايا المتحالفة: الزوايا المتحالفة الناتجة عن تقاطع مستقيمين متوازيين مع قاطع تكون متساوية.
3. يساوي الميل: المستقيمان اللذان لهما نفس الميل يعتبران متوازيين.
4. المسافة الثابتة: المسافة العمودية بين المستقيمين المتوازيين تبقى ثابتة على طول المستقيمات.

طرق إثبات توازي مستقيمين

إثبات التوازي بين مستقيمين يمكن تحقيقه باستخدام نظريات وقواعد هندسية متنوعة.

• استخدام نظرية الزوايا المتقابلة المتساوية

عند تقاطع قاطع لمستقيمين إذا كانت الزوايا المتقابلة الناشئة متساوية، فإن المستقيمين يكونان متوازيين.

• استخدام نظرية الزوايا المتبادلة الداخلية

إذا كانت الزوايا المتبادلة الداخلية بين مستقيمين تساوي بعضها البعض عند تقاطعهما مع قاطع، فإن المستقيمين يكونان متوازيين.

• استخدام الميل

إذا كان لمستقيمين نفس الميل، فإنهما يعتبران متوازيين، وتعتمد على المعادلات الخطية في المستوى.

• استخدام المسافة الثابتة

يمكن إثبات التوازي بين مستقيمين إذا كانت المسافة العمودية بينهما ثابتة على طول امتدادهما.

أمثلة تطبيقية على إثبات توازي مستقيمين

• المثال الأول: لنفترض وجود مستقيمين ABABAB وCDCDCD يتقاطعان مع قاطع EFEFEF بحيث تكون الزوايا المتبادلة الداخلية متساوية، وبالتالي يمكننا إثبات أن ABABAB وCDCDCD متوازيان.
• المثال الثاني: إذا كان لدينا معادلتين لمستقيمين على الشكل y=2x+3y = 2x + 3y=2x+3 وy=2x−5y = 2x – 5y=2x−5، حيث الميل هو نفسه، فيمكننا الاستنتاج أن المستقيمين متوازيين.

التطبيقات العملية لتوازي المستقيمات في الحياة

1. التصميم الهندسي: يُستخدم مفهوم التوازي في تصميم المباني والجسور لضمان استقرار الهياكل.
2. التخطيط العمراني: تُستخدم المستقيمات المتوازية في تصميم الطرق والشوارع بحيث تكون موازية لبعضها لتسهيل حركة السير.
3. الهندسة الميكانيكية: يُستخدم التوازي في صناعة الآلات لضمان تناغم حركة الأجزاء الميكانيكية.

التوازي في الأشكال الهندسية المختلفة

يُعتبر التوازي مبدأً أساسياً في تكوين العديد من الأشكال الهندسية مثل المستطيل، والمربع، والمتوازي الأضلاع، والمثلثات المتوازية.

• المستطيل والمربع

يتميز المستطيل بأن له زوجين من المستقيمات المتوازية، حيث يكون كل جانبين متقابلين متوازيين ومتساويين في الطول، وينطبق أيضاً على المربع، ولكنه يتميز بأن جوانبه الأربعة متساوية الطول.

• متوازي الأضلاع

هو شكل هندسي يحتوي على زوجين من الأضلاع المتوازية، وكل زوجين يكونان متساويين في الطول، ومن خلال معرفة متوازي الأضلاع يمكننا استنتاج خصائص الزوايا والأبعاد الداخلية لمتوازي الأضلاع.

• شبه المنحرف المتساوي الساقين

في هذا النوع من شبه المنحرف يكون هناك فقط زوج واحد من الأضلاع المتوازي، وتجعل من شبه المنحرف المتساوي الساقين مفيداً في العديد من التطبيقات الهندسية.

تطبيقات إثبات التوازي في الرياضيات والعلوم

التوازي ليس مجرد خاصية هندسية، بل هو أيضاً أداة مفيدة في الحسابات والمعادلات، وعلى سبيل المثال:

• في الرياضيات التحليلية

يمكن استخدام معادلات الخطوط المستقيمة في المستوى الديكارتي لإثبات التوازي حيث إنه إذا كان هناك مستقيمان لهما نفس الميل، فإنهما متوازيان

وعلى سبيل المثال في المعادلتين y=3x+5y = 3x + 5y=3x+5 وy=3x−7y = 3x – 7y=3x−7، نجد أن الميل هو 333 لكلا المستقيمين، مما يعني أنهما متوازيان.

• في الفيزياء

يستخدم التوازي لفهم حركة الأجسام ضمن الأطر المتوازية مثل السكك الحديدية، وفي مجال الكهرباء يستخدم في فهم التيارات الكهربائية في الدوائر المتوازية، حيث يتدفق التيار عبر أكثر من مسار واحد.

• في الرسم الهندسي والتصميم

يعد استخدام التوازي أساسياً في التصميم الهندسي والرسم المعماري، حيث يساعد المهندسين والمصممين على خلق تناغم بصري وتناسق بين الأشكال والهيكليات المختلفة.

استخدام البرهان الرياضي لإثبات توازي مستقيمين

يعتمد البرهان الرياضي على استخدام نظريات وحقائق رياضية لإثبات توازي مستقيمين، ومن بين أشهر البراهين المستخدمة:

البرهان عن طريق التناقض:

• يُستخدم البرهان بالتناقض عن طريق افتراض أن المستقيمين ليسا متوازيين، ثم التوصل إلى نتيجة متناقضة تثبت خطأ الافتراض الأصلي.
• إذا افترضنا أن مستقيمين يلتقيان في نقطة، ولكن باستخدام المعادلات الرياضية نكتشف أن الميلين متساويان، فإنه يؤدي إلى تناقض يؤكد أن المستقيمين متوازيان.

البرهان باستخدام التطابق:

• في بعض الأحيان يمكن إثبات التوازي باستخدام تطابق الزوايا.
• على سبيل المثال إذا تطابقت الزوايا المتبادلة أو المتحالفة الناتجة عن تقاطع مستقيمين مع قاطع، فإن ذلك يثبت توازي المستقيمين.

البرهان باستخدام خاصية المسافة الثابتة:

• إذا كان يمكننا إثبات أن المسافة بين المستقيمين ثابتة على طول امتدادهما، فإن هذا يعد دليلاً على أن المستقيمين متوازيان.

خاتمة بحث عن اثبات توازي مستقيمين

التوازي يلعب دوراً كبيراً في الهندسة الوصفية والفن البصري، وخاصة في التصوير الفوتوغرافي والرسم ثلاثي الأبعاد، ويمكن استخدامه لخلق تأثيرات بصرية تمثل العمق في الرسومات، حيث تستخدم الخطوط المتوازية لتوجيه عين المشاهد نحو نقطة التلاقي، مما يعطي انطباعاً بالمسافة والبعد.

اطلع على: بحث عن الدوال وأنواعه وأهميته كامل مع التحميل بصيغة Pdf