بحث كامل عن المحددات وقاعدة كرامر بصيغة PDF

تُعد المحددات من المفاهيم الرياضية المهمة التي تُستخدم في حل العديد من المسائل، خاصةً في مجال الجبر الخطي، وتأتي قاعدة كرامر كإحدى التطبيقات المهمة لهذه المحددات، إذ تُعد طريقة لحل الأنظمة الخطية من المعادلات بفاعلية.

يُمكنك تحميل بحث عن المحددات وقاعدة كرامر بصيغة pdf عبر:

مقدمة بحث عن المحددات

• المحدد هو قيمة حسابية تُستخرج من مصفوفة مربعة (مصفوفة ذات عدد متساوٍ من الصفوف والأعمدة).
• تُعد ذات أهمية خاصة في مجالات الرياضيات والفيزياء، حيث تُستخدم في حساب المساحات والأحجام وفي دراسة الأنظمة الخطية.
• يُعبَّر عن المحدد باستخدام أعداد مرتبة في مصفوفة مربعة، ويُرمز له غالبًا بالرمز |A| إذا كانت المصفوفة هي A.

خواص المحددات

للمحددات العديد من الخواص التي تسهل العمليات الحسابية وتساعد في تحليل الأنظمة الرياضية.

• التبديل بين الصفوف أو الأعمدة

إذا تم تبديل صفين أو عمودين في مصفوفة، فإن إشارة المحدد تتغير، بمعنى إذا كانت قيمة المحدد موجبة قبل التبديل، فإنها تصبح سالبة بعد التبديل والعكس صحيح.

• صف أو عمود يحتوي على أصفار

إذا كان صف أو عمود في المصفوفة يتكون بالكامل من أصفار، فإن قيمة المحدد تكون صفرًا، فهو لا يضيف قيمةً للمحدد.

• كرار الصفوف أو الأعمدة

إذا كان هناك صفان أو عمودان متطابقان في مصفوفة، فإن قيمة المحدد تساوي صفرًا، وهذا لأن التكرار يشير إلى عدم الاستقلال الخطي، مما يقلل من الرتبة ويجعل المحدد غير قابل للحساب كقيمة مختلفة عن الصفر.

• الضرب في ثابت

إذا ضُرب صف أو عمود معين في مصفوفة في ثابت معين، فإن قيمة المحدد تضرب في نفس هذا الثابت، وعلى سبيل المثال إذا تم ضرب صف واحد في 3، فإن قيمة المحدد تصبح ثلاثة أضعاف قيمته الأصلية.

• الخطية في الصفوف والأعمدة

المحدد يتصرف بطريقة خطية بالنسبة لكل صف أو عمود على حدة، وإذا كان لدينا صف (أو عمود) يمكن فصله إلى مجموع عددين أو أكثر، فيمكننا حساب المحدد كجمع لمحددات كل جزء على حدة.

• المحدد الناتج من جمع صفوف أو أعمدة

إذا تم جمع صفين أو عمودين في المصفوفة، فإن قيمة المحدد لا تتغير، وهذا يعني أن جمع صف أو عمود معين إلى صف أو عمود آخر لا يؤثر على قيمة المحدد.

• المحدد لمصفوفة مثلثية

إذا كانت المصفوفة مثلثية (مثلثية علوية أو مثلثية سفلية)، فإن المحدد يساوي حاصل ضرب عناصر القطر الرئيسي فقط، وهذا يسهل حساب المحدد للمصفوفات المثلثية، حيث لا تحتاج سوى ضرب قيم القطر.

• المحدد للمصفوفة المربعة من الدرجة \(n\)

لا يمكن حساب المحدد إلا للمصفوفات المربعة أي التي يكون عدد صفوفها مساويًا لعدد أعمدتها، وبالتالي إذا كانت المصفوفة ليست مربعة، فإن محددها غير مُعرف.

• التعامل مع مصفوفة الوحدة

إذا كانت المصفوفة هي مصفوفة الوحدة (Identity Matrix) التي تحتوي على أصفار في جميع المواقع باستثناء القطر الرئيسي (الذي يحتوي على آحاد)، فإن محدد هذه المصفوفة يساوي 1.

• محدد المصفوفة المعكوسة

إذا كانت \( A \) مصفوفة قابلة للعكس، فإن محدد معكوسها \( A^{-1} \) يساوي مقلوب محدد \( A \)، أي: |A^{-1}| = \frac{1}{|A|}

• محدد المصفوفة الناتجة عن الضرب

إذا كانت \( A \) و\( B \) مصفوفتين مربعتين من نفس الدرجة، فإن محدد حاصل الضرب \( AB \) يساوي حاصل ضرب محدديهما: |AB| = |A| \cdot |B|

• التغير بالإضافة الخطية

إذا تم إضافة مضاعف ثابت من صف إلى صف آخر (أو عمود إلى عمود آخر)، فإن قيمة المحدد لا تتغير.

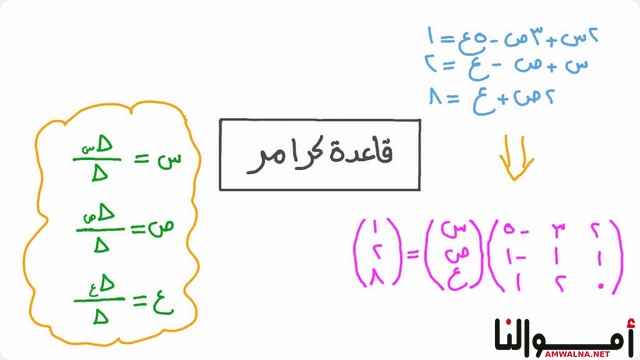
قاعدة كرامر لحل الأنظمة الخطية

هي طريقة لحل الأنظمة الخطية من المعادلات باستخدام المحددات، وتفيد في حل الأنظمة التي تحتوي على عدد معادلات يساوي عدد المتغيرات.

تُعتمد هذه القاعدة على تقسيم الأنظمة إلى مصفوفات فرعية، حيث يتم إنشاء مصفوفات جديدة من خلال استبدال أعمدة محددة في المصفوفة الأساسية بعمود الحلول.

تعريف قاعدة كرامر

إذا كان لدينا نظام خطي مكون من nnn معادلات وnnn متغيرات، يُمكن صياغته بالشكل: Ax=bAx = bAx=b حيث AAA هي مصفوفة المعاملات، وxxx هو متجه المتغيرات، وbbb هو متجه الحلول، وتُستخدم لحل هذا النظام إذا كانت قيمة محدد المصفوفة AAA لا تساوي صفرًا (∣A∣≠0|A| \neq 0∣A∣=0).

طريقة تطبيق قاعدة كرامر

لحل النظام باستخدام قاعدة كرامر:

1. نحسب محدد المصفوفة AAA، والذي سنرمز له بـ ∣A∣|A|∣A∣.
2. نقوم بتكوين مصفوفات فرعية AiA_iAi​، حيث يتم استبدال العمود iii في AAA بمتجه الحلول bbb.
3. نحسب محدد المصفوفة فرعية AiA_iAi​ للحصول على القيم ∣A1∣,∣A2∣,…,∣An∣|A_1|, |A_2|, \ldots, |A_n|∣A1​∣,∣A2​∣,…,∣An​∣.
4. حساب كل متغير xix_ixi​ باستخدام الصيغة: xi=∣Ai∣∣A∣x_i = \frac{|A_i|}{|A|}xi​=∣A∣∣Ai​∣​

تطبيقات قاعدة كرامر

قاعدة كرامر ليست فقط أداة رياضية مجردة، بل لها تطبيقات عملية في العديد من المجالات، مثل:

• الهندسة الكهربائية:

تُستخدم قاعدة كرامر لحل الأنظمة الخطية في تحليل الدوائر الكهربائية، وعلى سبيل المثال تُستخدم لحساب التيارات والجهود في الدوائر المعقدة التي تتكون من عدة مقاومات ومصادر جهد كما يمكن استخدامها لتحديد الجهود الكهربائية في نقاط مختلفة ضمن الشبكة.

• الميكانيكا والهندسة الإنشائية:

تُستخدم لحل الأنظمة الخطية المتعلقة بالقوى والعزوم التي تؤثر على الأجسام المتوازنة، وتساعد في حل الأنظمة الميكانيكية وتحليل الإطارات والأعمدة والرافعات لضمان استقرار الإنشاءات وحساب القوى المؤثرة على النقاط المختلفة.

• الاقتصاد:

تُستخدم لحل نماذج التوازن الاقتصادي التي تتضمن معادلات خطية، وتُستخدم لتحديد كيفية توزيع الإنتاج والموارد ضمن نظام اقتصادي معين، وأيضًا في تحليل الأسواق الاقتصادية والقرارات المتعلقة بالتكلفة والعائد.

• الفيزياء:

في العديد من التطبيقات الفيزيائية مثل دراسة الحركة وتحليل القوى تساعد قاعدة كرامر في حل الأنظمة الخطية المعقدة، وتُستخدم أيضًا في ميكانيكا الكم ومعادلات الحقل الكهربائي والمغناطيسي لتحديد القيم المرتبطة بالسرعة والتسارع والضغط في الأنظمة المختلفة.

• علوم الحاسوب والرسومات ثلاثية الأبعاد:

تُستخدم في الرسومات الحاسوبية لتحديد إحداثيات نقاط معينة، مما يساعد في بناء وتحريك الأشكال ثلاثية الأبعاد، وتُعد مفيدة في تطبيقات المحاكاة والتصميم الحاسوبي، حيث تسهم في رسم الصور والمجسمات بدقة.

• إدارة الأعمال:

تُستخدم قاعدة كرامر أحيانًا في مجال اتخاذ القرارات وحل المشاكل في الإدارة، حيث يكون هناك حاجة إلى حل أنظمة خطية لتحديد النسب المثلى للموارد والتوزيع الأمثل في تخطيط الموارد أو تحليل الربحية.

• تحليل الشبكات والأنظمة:

تُساعد في تحليل شبكات التدفق مثل شبكات النقل والمواصلات، وشبكات المياه والكهرباء، وشبكات الإنترنت، ويمكن استخدامها لتحليل تدفقات المعلومات وتوزيعها بشكل فعال، وكذلك لتقدير التدفقات التي تضمن الاستقرار والكفاءة في الأنظمة.

خاتمة بحث عن المحددات وقاعدة كرامر

على الرغم من فاعلية قاعدة كرامر، إلا أن لها بعض القيود:

• تعقيد الحسابات: تصبح عملية الحساب معقدة جدًا عند التعامل مع أنظمة ذات عدد كبير من المتغيرات.
• عدم القابلية للتطبيق في بعض الأنظمة: لا يمكن استخدام قاعدة كرامر إذا كان محدد مصفوفة المعاملات يساوي صفرًا، حيث يصبح النظام غير قابل للحل بالطريقة التقليدية.

اطلع على: بحث عن الدوال وأنواعه وأهميته كامل مع التحميل بصيغة Pdf